Alex tools

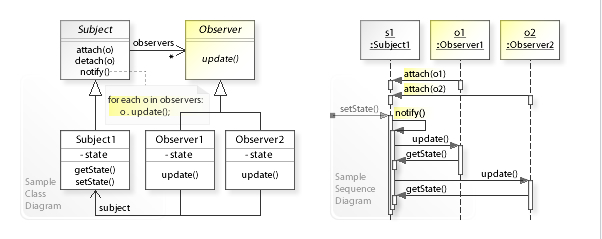
Паттерн наблюдатель (Observer) - это паттерн проектирования программного обеспечения, в котором объект, называемый субъектом, ведет список своих зависимых, называемых наблюдателями, и автоматически уведомляет их о любых изменениях состояния, обычно вызывая один из их методов. Он в основном используется для реализации распределенных систем обработки событий в программном обеспечении, "управляемом событиями" (event driven). В этих системах субъект обычно называется "потоком событий" или "источником событий", в то время как наблюдатели называются "приемниками событий". Номенклатура потока имитирует или адаптируется к физической установке, где наблюдатели физически разделены и не контролируют испускаемые события субъекта/источника потока. Этот паттерн идеально подходит для любого процесса, где данные поступают через ввод/вывод, то есть когда данные недоступны ЦПУ при запуске, но могут поступать "случайно" (HTTP-запросы, данные GPIO, ввод

Существует много типов двоичных деревьев поиска. Деревья AVL и красно-черные деревья являются формами самобалансирующихся двоичных деревьев поиска. Splay дерево - это двоичное дерево поиска, которое автоматически перемещает часто используемые элементы ближе к корню. В treap (куче дерева) каждый узел также имеет (случайно выбранный) приоритет, а родительский узел имеет более высокий приоритет, чем его дочерние элементы. Деревья танго - это деревья, оптимизированные для быстрого поиска. T-деревья - это двоичные деревья поиска, оптимизированные для сокращения объема памяти, широко используемые для баз данных в памяти. Вырожденное дерево - это дерево, в котором для каждого родительского узла существует только один связанный дочерний узел. Он неуравновешен и, в худшем случае, производительность снижается по сравнению со связным списком. Если ваша функция добавления узла не обрабатывает перебалансировку, то вы можете легко построить вырожденное дерево, передав его уже отсортированным данным

Сортировка Бинарное дерево поиска может быть использовано для реализации простого алгоритма сортировки. Как и в случае с heapsort, мы вставляем все значения, которые мы хотим отсортировать, в новую упорядоченную структуру данных - в данном случае это двоичное дерево поиска - и затем перемещаемся по порядку. Наихудшее время для build_binary_tree - O(n*n) - если вы передаете ему отсортированный список значений, он объединяет их в связанный список без левых поддеревьев. Например, build_binary_tree ([1, 2, 3, 4, 5]) выдает дерево (1 (2 (3 (4 (5)))))). Есть несколько схем для преодоления этого недостатка с помощью простых бинарных деревьев; наиболее распространенным является самобалансирующееся двоичное дерево поиска. Если эта же процедура выполняется с использованием такого дерева, общее время наихудшего случая составляет O(n log n), что является асимптотически оптимальным для сортировки сравнения. На практике добавленные издержки во времени и пространстве для сортировки на основе дерев

Иногда у нас уже есть двоичное дерево, и нам нужно определить, является ли оно BST (Binary Search Tree, двоичное дерево поиска). Эта проблема имеет простое рекурсивное решение. Свойство BST - каждый узел в правом поддереве должен быть больше текущего узла, а каждый узел в левом поддереве должен быть меньше текущего узла - является ключом к выяснению, является ли дерево BST или нет. Жадный (greedy) алгоритм - просто обход дерева, на каждом узле проверка, содержит ли узел значение, большее, чем значение у левого дочернего элемента и меньше, чем значение у правого дочернего элемента, - не работает во всех случаях. Рассмотрим следующее дерево: 20 / \ 10 30 / \ 5 40 В приведенном выше дереве каждый узел удовлетворяет условию, что узел содержит значение, большее, чем его левый дочерний элемент, и меньше, чем его правый дочерний элемент, и все же это не BST: значение 5 находится в правом поддереве узла, содержащего 20 , нарушение свойства BST. Вместо тог

Как только двоичное дерево поиска создано, его элементы могут быть извлечены по порядку путем рекурсивного обхода левого поддерева корневого узла, доступа к самому узлу, а затем рекурсивного обхода правого поддерева узла, продолжая этот шаблон для каждого узла в дерево как рекурсивное обращение. Как и во всех двоичных деревьях, можно выполнить обход до или после обхода, но ни один из них, вероятно, не будет полезен для деревьев двоичного поиска. Упорядоченный обход двоичного дерева поиска всегда приводит к отсортированному списку элементов узлов (чисел, строк или других сопоставимых элементов). Код для обхода по порядку в Python приведен ниже. Он будет вызывать обратный вызов (некоторая функция, которую программист желает вызвать по значению узла, например, вывод на экран) для каждого узла в дереве. def traverse_binary_tree(node, callback): if node is None: return traverse_binary_tree(node.leftChild, callback) callback(node.value) traverse_binary_tree(node.

При удалении узла из бинарного дерева поиска обязательно поддерживать последовательность узлов в порядке. Есть много возможностей сделать это. Однако следующий метод, который был предложен Т. Хиббардом в 1962 г., гарантирует, что высота поддеревьев субъекта изменяется не более чем на единицу. Есть три возможных случая для рассмотрения: Удаление узла без дочерних элементов: просто удалите узел из дерева. Удаление узла с одним дочерним узлом: удалите узел и замените его дочерним. Удаление узла с двумя дочерними элементами: вызов узла, подлежащего удалению D. Не удаляйте D. Вместо этого выберите либо его предшествующий узел по порядку, либо его последующий узел по порядку в качестве заменяющего узла E. Скопируйте пользовательские значения E в D. Если E не имеет дочернего элемента, просто удалите E из своего предыдущего родителя G. Если E имеет дочерний элемент, скажем F, это правильный дочерний элемент. Замените E на F у родителя E. Во всех случаях, когда D оказывается корневым, сно

Вставка начинается так же, как начинается поиск; если ключ не равен ключу корня, мы ищем левое или правое поддерево, как и раньше. В конце концов, мы достигнем внешнего узла и добавим новую пару ключ-значение (здесь закодированную как запись 'newNode') в качестве его правого или левого потомка, в зависимости от ключа узла. Другими словами, мы проверяем корень и рекурсивно вставляем новый узел в левое поддерево, если его ключ меньше ключа корня, или правое поддерево, если его ключ больше или равен корню. Вот как типичная вставка двоичного дерева поиска может выполняться в двоичном дереве в C++: void insert(Node*& root, int key, int value) { if (!root) root = new Node(key, value); else if (key == root->key) root->value = value; else if (key < root->key) insert(root->left, key, value); else // key > root->key insert(root->right, key, value); } В качестве альтернативы, нерекурсивная версия может быть реализована следующи

Двоичные деревья поиска поддерживают три основных операции: вставка элементов, удаление элементов и поиск (проверка наличия ключа). Поиск Поиск в двоичном дереве поиска конкретного ключа может быть запрограммирован рекурсивно или итеративно. Начнем с изучения корневого узла. Если дерево является нулевым, ключ, который мы ищем, не существует в дереве. Иначе, если ключ равен ключу корня, поиск успешен, и мы возвращаем узел. Если ключ меньше, чем у корня, мы ищем левое поддерево. Точно так же, если ключ больше, чем ключ корня, мы ищем в правом поддереве. Этот процесс повторяется до тех пор, пока ключ не будет найден или оставшееся поддерево будет нулевым. Если искомый ключ не найден после того, как достигнуто нулевое поддерево, этот ключ отсутствует в дереве. Это легко выразить как рекурсивный алгоритм (реализованный на Python): def search_recursively(key, node): if node is None or node.key == key: return node if key < node.key: return search_recursively(

В информатике двоичные деревья поиска (BST, binary search tree) , иногда называемые упорядоченными или отсортированными двоичными деревьями, представляют собой особый тип контейнера: структуру данных, которая хранит "элементы" (такие как числа, имена и т. д.) в памяти. Они позволяют осуществлять быстрый поиск, добавление и удаление элементов и могут использоваться для реализации либо динамических наборов элементов, либо таблиц поиска, которые позволяют найти элемент по его ключу (например, найти номер телефона человека по имени). Деревья бинарного поиска хранят свои ключи в отсортированном порядке, так что поиск и другие операции могут использовать принцип бинарного поиска: при поиске ключа в дереве (или месте для вставки нового ключа) они пересекают дерево от корня до листьев, делая сравнения с ключами, хранящимися в узлах дерева и решая, на основе сравнения, продолжить поиск в левом или правом поддеревьях. В среднем это означает, что каждое сравнение позволяет операциям пр

В дополнение к его использованию в базах данных, B-дерево также используется в файловых системах, чтобы обеспечить быстрый произвольный доступ к произвольному блоку в определенном файле. Основная проблема заключается в том, чтобы превратить адрес файла i в адрес блока диска (или, возможно, в сектор головки цилиндров). Некоторые операционные системы требуют, чтобы пользователь выделял максимальный размер файла при его создании. Затем файл может быть выделен как непрерывные блоки диска. В этом случае, чтобы преобразовать адрес блока файла i в адрес блока диска, операционная система просто добавляет адрес блока файла i к адресу первого блока диска, составляющего файл. Схема проста, но файл не может превышать созданный размер. Другие операционные системы позволяют файлу расти. Результирующие дисковые блоки могут не быть смежными, поэтому отображение логических блоков на физические блоки является более сложным. MS-DOS, например, использовал простую таблицу размещения файлов (FAT). FAT им

Поиск Поиск похож на поиск в двоичном дереве поиска. Начиная с корня, дерево рекурсивно перемещается сверху вниз. На каждом уровне поиск сокращает свое поле зрения до дочернего указателя (поддерева), диапазон которого включает значение поиска. Диапазон поддерева определяется значениями или ключами, содержащимися в его родительском узле. Эти предельные значения также известны как значения разделения. Бинарный поиск обычно (но не обязательно) используется в узлах, чтобы найти значения разделения и интересующее дочернее дерево. Вставка Все вставки начинаются с конечного узла. Чтобы вставить новый элемент, выполните поиск в дереве, чтобы найти листовой узел, в который должен быть добавлен новый элемент. Вставьте новый элемент в этот узел, выполнив следующие действия: Если узел содержит меньше максимально допустимого количества элементов, тогда есть место для нового элемента. Вставьте новый элемент в узел, сохраняя элементы узла в порядке. В противном случае узел заполнен, равномерно

Литература о B-деревьях неоднородна по своей терминологии (Folk & Zoellick 1992). Bayer&McCreight (1972), Comer (1979) и другие определяют порядок B-дерева как минимальное количество ключей в некорневом узле. Фолк и Зеллик (1992) указывают, что терминология неоднозначна, поскольку максимальное количество ключей не ясно. B-дерево порядка 3 может содержать максимум 6 ключей или максимум 7 ключей. Кнут (1998) избегает этой проблемы, определяя порядок как максимальное число дочерних элементов (что на один больше, чем максимальное количество ключей). Термин "лист"(leaf) также противоречив. Bayer & McCreight (1972) рассматривали уровень листа как самый низкий уровень ключей, но Кнут считал уровень листа на один уровень ниже самых низких ключей (Folk & Zoellick 1992). Есть много возможных вариантов реализации. В некоторых проектах листья могут содержать всю запись данных; в других реализациях листья могут содержать только указатели на запись данных. Эти выборы не я

Время для поиска отсортированного файла Обычно алгоритмы сортировки и поиска характеризуются количеством операций сравнения, которые должны быть выполнены с использованием записи порядка. Например, двоичный поиск отсортированной таблицы с N записями может быть выполнен примерно в log2 N сравнениях. Если в таблице содержится 1 000 000 записей, то конкретная запись может быть найдена не более чем в 20 сравнениях: log2 (1 000 000) = 20. Исторически большие базы данных хранились на дисках. Время чтения записи на диске намного превышает время, необходимое для сравнения ключей, когда запись становится доступной. Время чтения записи с дисковода включает время поиска и задержку вращения. Время поиска может составлять от 0 до 20 или более миллисекунд, а задержка вращения составляет в среднем около половины периода вращения. Для привода 7200 об/мин период вращения составляет 8,33 миллисекунды. Для такого привода, как Seagate ST3500320NS, время поиска между дорожками составляет 0,8 миллисекун

В информатике B-дерево (B-tree) - это самобалансирующаяся древовидная структура данных, которая поддерживает отсортированные данные и позволяет осуществлять поиск, последовательный доступ, вставки и удаления в логарифмическом времени. B-дерево - это обобщение бинарного дерева поиска, в котором у узла может быть более двух дочерних элементов. В отличие от других самобалансирующихся бинарных деревьев поиска, B-дерево хорошо подходит для систем хранения, которые читают и записывают относительно большие блоки данных, такие как диски. Обычно используется в базах данных и файловых системах. То, за что означает B, никогда не было установлено. Происхождение B-деревья были изобретены Рудольфом Байером и Эдвардом М. МакКрейтом в 1970 году с целью эффективного управления индексными страницами для больших файлов с произвольным доступом. Основное предположение заключалось в том, что индексы будут настолько объемными, что только небольшие куски дерева могут поместиться в основной памяти. Первая