Хэш-таблица: разрешение коллизий

Хэш-коллизии практически неизбежны при хэшировании случайного подмножества большого набора возможных ключей. Например, если 2450 ключей хэшируются в миллион корзин (buckets), даже при совершенно равномерном случайном распределении, в соответствии с проблемой дня рождения, существует приблизительно 95% вероятность того, что по крайней мере два ключа будут хэшированы в один и тот же слот.

Поэтому почти все реализации хэш-таблиц имеют некоторую стратегию разрешения коллизий для обработки таких событий. Некоторые общие стратегии описаны ниже. Все эти методы требуют, чтобы ключи (или указатели на них) были сохранены в таблице вместе со связанными значениями.

Отдельная цепочка

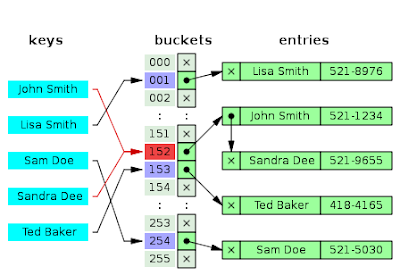
В методе, известном как отдельная цепочка, каждая корзина (bucket) независима и имеет своего рода список записей с одинаковым индексом. Время для операций с хэш-таблицами - это время нахождения корзины (bucket) (которое является постоянным) плюс время для операции со списком.

В хорошей хэш-таблице каждая корзина (bucket) имеет ноль или одну запись, а иногда две или три, но редко больше. Поэтому структуры, которые эффективны во времени и пространстве для этих случаев, являются предпочтительными. Структуры, которые эффективны для довольно большого количества записей на корзину, не нужны или нежелательны. Если такие случаи случаются часто, хэширующая функция должна быть исправлена.

Отдельное сцепление со связанными списками

Связанные хэш-таблицы со связанными списками популярны, потому что они требуют только базовых структур данных с простыми алгоритмами и могут использовать простые хэш-функции, которые не подходят для других методов.

Стоимость табличной операции заключается в сканировании записей выбранной корзины для требуемого ключа. Если распределение ключей достаточно равномерное, средняя стоимость поиска зависит только от среднего числа ключей в каждой корзине, то есть приблизительно пропорциональна коэффициенту загрузки.

По этой причине цепочечные хэш-таблицы остаются в силе даже тогда, когда количество записей таблицы n намного больше, чем количество временных интервалов. Например, цепочечная хэш-таблица с 1000 слотов и 10000 хранимых ключей (коэффициент загрузки 10) в пять-десять раз медленнее, чем таблица с 10000 слотов (коэффициент загрузки 1); но все же в 1000 раз быстрее, чем простой последовательный список.

Для отдельной цепочки в худшем случае, когда все записи вставляются в одну корзину, хэш-таблица неэффективна, а стоимость поиска равна стоимости поиска структуры данных корзины. Если последний представляет собой линейный список, процедуре поиска может потребоваться отсканировать все его записи, поэтому стоимость наихудшего случая пропорциональна количеству n записей в таблице.

Цепочки корзины часто ищутся последовательно, используя порядок, в котором записи были добавлены в корзину. Если коэффициент загрузки велик, и некоторые ключи, скорее всего, появятся, вероятней чем другие, то может быть эффективным перераспределение цепи с эвристикой перемещения вперед. Более сложные структуры данных, такие как сбалансированные деревья поиска, заслуживают рассмотрения, только если коэффициент загрузки велик (около 10 или более), или если распределение хэша, вероятно, будет очень неоднородным, или если нужно гарантировать хорошую производительность даже в худшем случае. Однако использование таблицы большего размера и/или лучшей хэш-функции может быть даже более эффективным в этих случаях.

Связанные хэш-таблицы также наследуют недостатки связанных списков. При хранении маленьких ключей и значений, пространство надстроек следующего указателя в каждой записи может быть значительным. Дополнительным недостатком является то, что обход связанного списка имеет низкую производительность кэша, что делает кэш процессора неэффективным.

Отдельное сцепление со списком заголовочных ячеек

Некоторые реализации цепочки хранят первую запись каждой цепочки в самом массиве слотов. Количество обходов указателей в большинстве случаев уменьшается на единицу. Целью является повышение эффективности кэширования доступа к хэш-таблицам.

Недостатком является то, что пустая корзина занимает то же место, что и корзина с одним входом. Чтобы сэкономить место, такие хэш-таблицы часто имеют столько же слотов, сколько и сохраненных записей, а это означает, что во многих слотах есть две или более записей.

Отдельное сцепление с другими структурами

Вместо списка можно использовать любую другую структуру данных, которая поддерживает требуемые операции. Например, используя самобалансирующееся двоичное дерево поиска, теоретическое время наихудшего случая операций с обычной хэш-таблицей (вставка, удаление, поиск) может быть уменьшено до O(log n), а не O(n). Однако это вносит дополнительную сложность в реализацию и может привести к еще худшей производительности для небольших хэш-таблиц, где время, затрачиваемое на вставку и балансировку дерева, больше, чем время, необходимое для выполнения линейного поиска по всем элементам списка. Реальным примером хэш-таблицы, которая использует самобалансирующееся двоичное дерево поиска для сегментов, является класс HashMap в Java 8.

Вариант, называемый хэш-таблицей массива, использует динамический массив для хранения всех записей, хэширующих в одном и том же слоте. Каждая вновь вставленная запись добавляется в конец динамического массива, назначенного слоту. Размер динамического массива изменяется точно, то есть он увеличивается только на столько байтов, сколько необходимо. Было обнаружено, что альтернативные методы, такие как увеличение массива по размерам блоков или страниц, улучшают производительность вставки, но с затратами в пространстве. Это изменение позволяет более эффективно использовать кеширование процессора и буфер трансляций (TLB), поскольку записи слотов хранятся в последовательных позициях памяти. Он также обходится без следующих указателей, которые требуются для связанных списков, что экономит место. Несмотря на частое изменение размера массива, было обнаружено, что накладные расходы, связанные с операционной системой, такие как фрагментация памяти, невелики.

Детализация этого подхода - так называемое динамическое идеальное хэширование, где сегмент, содержащий k записей, организован в виде идеальной хэш-таблицы с k*k слотами. Хотя он использует больше памяти (n*n слотов для n записей, в худшем случае и n*k слотов в среднем случае), этот вариант имеет гарантированное постоянное время поиска в худшем случае и низкое амортизированное время для вставки. Также возможно использовать дерево слияния для каждого сегмента, достигая постоянного времени для всех операций с высокой вероятностью.

Открытая адресация

В другой стратегии, называемой открытой адресацией, все записи хранятся в самом массиве корзин (buckets). Когда необходимо вставить новую запись, корзины проверяются, начиная с ячейки хэшированного до и продолжаясь в некоторой последовательности проб, до тех пор, пока не будет найден незанятый слот. При поиске записи корзины сканируются в той же последовательности, пока не будет найдена либо целевая запись, либо не найден слот неиспользуемого массива, что указывает на то, что в таблице такого ключа нет. Название "открытая адресация" относится к тому факту, что местоположение ("адрес") элемента не определяется его хэш-значением. (Этот метод также называется закрытым хэшированием; его не следует путать с "открытым хэшированием" или "закрытой адресацией", которые обычно означают отдельное сцепление.)

Хорошо известные последовательности проб включают в себя:

Линейное пробирование, в котором интервал между пробами фиксирован (обычно 1)
Квадратичное пробирование, в котором интервал между пробами увеличивается путем добавления последовательных выходных данных квадратичного полинома к начальному значению, заданному исходным вычислением хэша
Двойное хэширование, в котором интервал между зондами вычисляется второй хэш-функцией

Недостаток всех этих схем открытой адресации состоит в том, что количество сохраненных записей не может превышать количество временных интервалов в массиве сегментов. На самом деле, даже с хорошими хэш-функциями их производительность резко ухудшается, когда коэффициент загрузки превышает 0,7 или около того. Для многих приложений эти ограничения требуют использования динамического изменения размера с сопутствующими затратами.

Схемы открытой адресации также предъявляют более жесткие требования к хэш-функции: помимо более равномерного распределения ключей по сегментам, функция также должна минимизировать кластеризацию последовательных хэш-значений в порядке проверки. При использовании отдельной цепочки единственная проблема заключается в том, что слишком много объектов отображаются на одно и то же значение хэш-функции; являются ли они смежными или соседними, абсолютно не имеет значения.

Открытая адресация экономит память только в том случае, если записи небольшие (менее чем в четыре раза больше размера указателя) и коэффициент загрузки не слишком мал. Если коэффициент загрузки близок к нулю (т.е. корзин намного больше, чем сохраненных записей), открытая адресация расточительна, даже если каждая запись состоит всего из двух слов.

Следующий график сравнивает среднее количество пропусков кэша, необходимых для поиска элементов в таблицах с цепочкой и линейным зондированием. Когда таблица проходит отметку в 80%, производительность линейного зондирования резко ухудшается.

Открытая адресация позволяет избежать временных затрат на выделение каждой новой записи и может быть реализована даже в отсутствие распределителя памяти. Это также позволяет избежать лишнего косвенного обращения, необходимого для доступа к первой записи каждого сегмента (то есть обычно единственной). Он также имеет лучшую локацию, особенно с линейным пробированием. При небольших размерах записи эти факторы могут дать лучшую производительность, чем цепочка, особенно для поисков. Хэш-таблицы с открытой адресацией также легче сериализовать, потому что они не используют указатели.

С другой стороны, нормальная открытая адресация является плохим выбором для больших элементов, потому что эти элементы заполняют все строки кэша ЦП (сводя на нет преимущество в кэше), и большой объем памяти теряется на больших пустых слотах таблиц. Если открытая таблица адресации хранит только ссылки на элементы (внешнее хранилище), она использует пространство, сравнимое с цепочкой, даже для больших записей, но теряет свое преимущество в скорости.

Вообще говоря, открытую адресацию лучше использовать для хэш-таблиц с небольшими записями, которые могут храниться в таблице (внутреннее хранилище) и помещаться в строку кэша. Они особенно подходят для элементов одного слова или меньше. Если ожидается, что таблица будет иметь высокий коэффициент загрузки, записи будут большими или данные имеют переменный размер, цепочечные хэш-таблицы часто работают так же или лучше.

Объединенное хэширование

Гибрид цепочки и открытой адресации, объединенное хэширование связывает вместе цепочки узлов в самой таблице. Как и открытая адресация, оно обеспечивает использование пространства и (несколько уменьшенное) преимущество кэширования по сравнению с цепочкой. Как и цепочка, оно не обладает эффектом кластеризации; фактически таблица может быть эффективно заполнена до высокой плотности. В отличие от цепочки, оно не может иметь больше элементов, чем слотов таблиц.

Кукушечное хэширование

Другим альтернативным решением с открытой адресацией является хэширование кукушки, которое обеспечивает постоянное время поиска и удаления в худшем случае, а также постоянное амортизированное время для вставок (с низкой вероятностью, что будет встречаться худший случай). Оно использует две или более хэш-функций, что означает, что любая пара ключ/значение может находиться в двух или более местах. Для поиска используется первая хэш-функция; если ключ/значение не найдено, то используется вторая хэш-функция и т. д. Если во время вставки происходит коллизия, то ключ повторно хэшируется со второй хэш-функцией, чтобы сопоставить его с другой кориной. Если используются все хэш-функции и все еще существует коллизия, то ключ с которым произошла коллизия удаляется, чтобы освободить место для нового ключа, а старый ключ повторно хэшируется с одной из других хэш-функций, которая сопоставляет его с другой корзиной. Если это расположение также приводит к коллизии, то процесс повторяется до тех пор, пока не произойдет коллизия, или процесс не пройдет все корзины, после чего размер таблицы будет изменен. Комбинируя несколько хэш-функций с несколькими ячейками на сегмент, можно достичь очень высокого использования пространства.

Hopscotch хэширование

Другим альтернативным решением с открытой адресацией является хэширование классиков, которое сочетает в себе подходы хэширования кукушки и линейного пробирования, но в целом, похоже, позволяет избежать их ограничений. В частности, оно работает хорошо, даже когда коэффициент загрузки превышает 0,9. Алгоритм хорошо подходит для реализации изменяемой параллельной хэш-таблицы.

Алгоритм хэширования классиков работает путем определения окрестности корзин рядом с исходной корзиной хэширования, в которой всегда находится заданная запись. Таким образом, поиск ограничен числом записей в этой окрестности, которое является логарифмическим в худшем случае, постоянным в среднем и при правильном выравнивании окрестности обычно требует одного промаха кэша. При вставке записи сначала пытаются добавить ее в соседнюю корзину. Однако, если все корзины в этой окрестности заняты, алгоритм последовательно проходит корзины до тех пор, пока не будет найден открытый слот (незанятая корзина) (как при линейном пробировании). В этот момент, поскольку пустая корзина находится за пределами окрестности, элементы многократно перемещаются в последовательности прыжков. (Это похоже на хэширование кукушки, но с той разницей, что в этом случае пустой слот перемещается по соседству, вместо того, чтобы перемещать предметы с надеждой найти в конечном итоге пустой слот.) Каждый прыжок приближает открытый слот в исходную окрестность, не аннулируя свойство окрестности любой из корзин пути. В конце концов, открытый слот был перемещен в окрестность, и вставляемая запись может быть добавлена в него.

Хэширование Робина Гуда

Одним из интересных вариантов разрешения коллизий с двойным хэшированием является хэширование Робина Гуда. Идея состоит в том, что новый ключ может сместить уже вставленный ключ, если его счетчик больше, чем у ключа в текущей позиции. Общий эффект состоит в том, что это уменьшает время поиска в худшем случае в таблице. Это похоже на упорядоченные хэш-таблицы, за исключением того, что критерий столкновения с ключом не зависит от прямой связи между ключами. Поскольку и наихудший случай, и разброс количества проб значительно сокращены, интересным вариантом является исследование таблицы, начиная с ожидаемого успешного значения пробы, а затем расширение из этой позиции в обоих направлениях. Внешнее хэширование Робина Гуда является расширением этого алгоритма, когда таблица хранится во внешнем файле, и каждая позиция таблицы соответствует странице или корзине фиксированного размера с записями B.

Двухвариантное хэширование

Хэширование с 2 вариантами выбора использует две разные хэш-функции, h1(x) и h2(x), для хэш-таблицы. Обе хэш-функции используются для вычисления двух положений таблицы. Когда объект вставляется в таблицу, он помещается в местоположение таблицы, которое содержит меньше объектов (по умолчанию используется местоположение таблицы h1(x), если есть равенство размера корзины). В хэшировании с двумя вариантами применяется принцип степени двух вариантов.

Поиск по этому блогу

Alex tools