Структуры данных: связанный список
В информатике связанный список - это линейный набор элементов данных, порядок которых не определяется их физическим размещением в памяти. Вместо этого каждый элемент указывает на следующий. Это структура данных, состоящая из набора узлов, которые вместе представляют последовательность. В своей основной форме каждый узел содержит: данные и указатель (другими словами, ссылку) на следующий узел в последовательности. Эта структура позволяет эффективно вставлять или удалять элементы из любой позиции в последовательности во время итерации. Более сложные варианты добавляют дополнительные ссылки, позволяя более эффективно вставлять или удалять узлы в произвольных положениях. Недостатком связанных списков является то, что время доступа является линейным. Более быстрый доступ, такой как произвольный доступ, невозможен. Массивы имеют лучшую локальность кэша по сравнению со связанными списками.
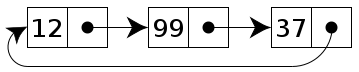
На схеме изображен связанный список, узлы которого содержат два поля: целочисленное значение и ссылку на следующий узел. Последний узел связан с терминатором, используемым для обозначения конца списка.
Связанные списки являются одними из самых простых и распространенных структур данных. Они могут быть использованы для реализации нескольких других общих абстрактных типов данных, включая списки, стеки, очереди, ассоциативные массивы и S-выражения, хотя весьма обычно реализовывать эти структуры данных напрямую, не используя связанный список в качестве основы.
Основное преимущество связанного списка по сравнению с обычным массивом состоит в том, что элементы списка могут быть легко вставлены или удалены без перераспределения или реорганизации всей структуры, потому что элементы данных не должны храниться непрерывно в памяти или на диске, в то время как реструктуризация массива во время выполнения - намного более дорогая операция. Связанные списки позволяют вставлять и удалять узлы в любой точке списка и позволяют делать это с постоянным числом операций, сохраняя ссылку, предшествующую ссылке, добавляемой или удаляемой в памяти во время обхода списка.
С другой стороны, поскольку простые связанные списки сами по себе не допускают произвольного доступа к данным или какой-либо формы эффективной индексации, многие основные операции, такие как получение последнего узла списка, поиск узла, содержащего заданную точку данных, или поиск места, где должен быть вставлен новый узел - может потребовать итерации большинства или всех элементов списка. Преимущества и недостатки использования связанных списков приведены ниже.
Преимущества
- Связанные списки являются динамическими, поэтому длина списка может увеличиваться или уменьшаться по мере необходимости. Каждый узел не обязательно следует за предыдущим физически в памяти.
- Позволяют выполнять эффективные операции удаления и вставки.
Недостатки
- Они используют больше памяти, чем массивы из-за памяти, используемой их указателями.
- Узлы в связанном списке должны читаться по порядку с самого начала, так как связанные списки по своей сути являются последовательным доступом.
- Узлы хранятся непоследовательно, что значительно увеличивает периоды времени, необходимые для доступа к отдельным элементам в списке, особенно с использованием кэша ЦП.
- Трудности возникают в связанных списках, когда дело доходит до обратного обхода. Например, односвязные списки неудобны для навигации назад, и хотя двусвязные списки несколько проще для чтения, память используется для выделения места для обратного указателя.
История
Связанные списки были разработаны в 1955–1956 гг. Алленом Ньюэллом, Клиффом Шоу и Гербертом А. Саймоном в RAND Corporation в качестве основной структуры данных для их языка обработки информации. Авторы использовали IPL для разработки нескольких ранних программ искусственного интеллекта, в том числе машины теории логики, решения общих проблем и компьютерной шахматной программы. Отчеты об их работе появились в "Операции IRE по теории информации" в 1956 году, а также в нескольких материалах конференций с 1957 по 1959 годы, в том числе в "Сводных данных по Западной компьютерной конференции в 1957 и 1958 годах" и "Обработка информации" (Материалы первой международной конференции ЮНЕСКО по обработке информации) в 1959 году. Классическая диаграмма, состоящая из блоков, представляющих узлы списка со стрелками, указывающими на последовательные узлы списка, появилась в "Программировании машины теории логики" Ньюэлла и Шоу, февраль 1957 года. Ньюэлл и Саймон были награждены премией ACM Turing в 1975 году за то, что они "внесли основной вклад в искусственный интеллект, психологию человеческого познания и обработку списков". Проблема машинного перевода для обработки естественного языка привела к тому, что Виктор Ингве из Массачусетского технологического института (MIT) использовал связанные списки в качестве структур данных в своем языке программирования COMIT для компьютерных исследований в области лингвистики. Отчет по этому языку под названием "Язык программирования для механического перевода" появился в "Механическом переводе" в 1958 году.
LISP, обозначающий "обработчик списков" (list processor), был создан Джоном Маккарти в 1958 году, когда он работал в MIT, а в 1960 году он опубликовал свой дизайн в статье в "Сообщения ACM", озаглавленной "Рекурсивные функции символьных выражений и их вычисление на машине, часть I". Одна из основных структур данных LISP - это связанный список.
К началу 1960-х годов, использование как связанных списков, так и языков, которые используют эти структуры в качестве своего основного представления данных, было хорошо установлено. Берт Грин из MIT Lincoln Laboratory опубликовал обзорную статью под названием "Компьютерные языки для манипулирования символами" в "Сделки IRE по человеческому фактору в электронике" в марте 1961 года, в которой обобщены преимущества подхода связанного списка. Поздняя обзорная статья Боброу и Рафаэля "Сравнение компьютерных языков для обработки списков" появилась в Communications of ACM в апреле 1964 года.
Некоторые операционные системы, разработанные Technical Systems Consultants (первоначально из West Lafayette Indiana, а затем из Chapel Hill, Северная Каролина), использовали односвязные списки в качестве файловых структур. Запись в каталоге указала на первый сектор файла, и последующие части файла были найдены с помощью обходных указателей. Системы, использующие эту технику, включают Flex (для процессора Motorola 6800), mini-Flex (тот же процессор) и Flex9 (для процессора Motorola 6809). Вариант, разработанный TSC для компании Smoke Signal Broadcasting в Калифорнии таким же образом, использует двусвязные списки.
Операционная система TSS/360, разработанная IBM для компьютеров System 360/370, использовала двойной связанный список для своего каталога файловой системы. Структура каталогов была похожа на Unix, где каталог мог содержать файлы и другие каталоги и распространяться на любую глубину.
Основные понятия
Каждая запись связанного списка часто называется "элементом" (element) или "узлом" (node).
Поле каждого узла, которое содержит адрес следующего узла, обычно называется "следующая ссылка" (next link) или "следующий указатель" (next pointer). Остальные поля называются полями "данные" (data), "информация" (information), "значение" (value), "груз" (cargo) или "полезная нагрузка" (payload).
"Голова" (head) списка - это его первый узел. "Хвост" (tail) списка может относиться либо к остальной части списка после заголовка, либо к последнему узлу в списке. В Lisp и некоторых производных языках следующий узел может называться 'cdr' (произносится could-er) списка, а полезная нагрузка головного узла может называться 'car'.
Единственно связанный список (Singly linked list, Односвязный список)
Односвязные списки содержат узлы, которые имеют поле данных, а также поле "следующий", которое указывает на следующий узел в строке узлов. Операции, которые могут выполняться в односвязных списках, включают вставку, удаление и обход.
Следующий Java код демонстрирует простую реализацию односвязного списка с методами вставки и обхода:
public class SinglyLinkedList {
// Узел односвязного списка
class Node {
int data;
Node next;
public Node(int data) {
this.data = data;
this.next = null;
}
}
// Голова и хвост односвязного списка
public Node head = null;
public Node tail = null;
// addNode() добавляет новый узел в список
public void addNode(int data) {
// Создаем новый узел
Node newNode = new Node(data);
// Проверяем не пустой ли список
if(head == null) {
// Если список пустой,
// голова и хвост будут указывать
// на новый узел
head = newNode;
tail = newNode;
} else {
// newNode будет добавлен в хвост,
// так что next будет указывать на newNode
tail.next = newNode;
// newNode станет новым хвостом списка
tail = newNode;
}
}
// traverse() будет отображать все узлы,
// присуствующие в списке
public void traverse() {
// Узел current указывает на голову
Node current = head;
if(head == null) {
System.out.println("Список пуст");
return;
}
System.out.println("Узлы односвязного списка: ");
while(current != null) {
// Печатаем каждый узел
System.out.print(current.data + " ");
current = current.next;
}
System.out.println();
}
}
Двусвязный список
В двусвязном списке каждый узел содержит, помимо ссылки на следующий узел, второе поле ссылки, указывающее на предыдущий узел в последовательности.
Методика, известная как XOR-связывание (XOR-linking), позволяет реализовать двусвязный список с использованием одного поля ссылки в каждом узле. Однако этот метод требует возможности выполнять битовые операции с адресами и поэтому может быть недоступен на некоторых языках высокого уровня.
Многие современные операционные системы используют двусвязные списки для поддержки ссылок на активные процессы, потоки и другие динамические объекты. Обычной стратегией, позволяющей руткитам уклоняться от обнаружения, является отсоединение себя от этих списков.
Многосвязный список
В многосвязном списке каждый узел содержит два или более полей ссылок, каждое из которых используется для подключения одного и того же набора записей данных в различном порядке одного и того же набора (например, по имени, по отделу, по дате рождения, и т.д.). Хотя двусвязные списки можно рассматривать как особые случаи многосвязных списков, тот факт, что два и более порядков противоположны друг другу, приводит к более простым и более эффективным алгоритмам, поэтому они обычно рассматриваются как отдельный случай.
Круговой связанный список
В последнем узле списка поле ссылки часто содержит нулевую ссылку, специальное значение используется для указания отсутствия других узлов. Менее распространенное соглашение - указывать на первый узел списка; в этом случае список называется "круговым" или "циклически связанным"; в противном случае он называется "открытым" или "линейным". Круговой связанный список - это список, где последний указатель указывает на первый узел.
В случае кругового двусвязного списка первый узел также указывает на последний узел списка.
Часовые узлы (Sentinel nodes)
В некоторых реализациях дополнительный "дозорный" или "фиктивный" узел может быть добавлен перед первой записью данных или после последней. Это соглашение упрощает и ускоряет некоторые алгоритмы обработки списков, гарантируя, что все ссылки могут быть безопасно разыменованы, и что каждый список (даже тот, который не содержит элементов данных) всегда имеет "первый" и "последний" узел.
Пустые списки
Пустой список - это список, который не содержит записей данных. Обычно это то же самое, что сказать, что у него ноль узлов. Если используются сторожевые узлы, список обычно называют пустым, если в нем есть только сторожевые узлы.
Хэш-связь
Поля связи не обязательно должны быть физически частью узлов. Если записи данных хранятся в массиве и на них ссылаются их индексы, поле ссылки может храниться в отдельном массиве с теми же индексами, что и записи данных.
Список ручек
Поскольку ссылка на первый узел дает доступ ко всему списку, эту ссылку часто называют "адресом", "указателем" или "дескриптором" списка. Алгоритмы, которые управляют связанными списками, обычно получают такие дескрипторы в списки ввода и возвращают дескрипторы в результирующие списки. Фактически, в контексте таких алгоритмов слово "список" часто означает "дескриптор списка". В некоторых ситуациях, однако, может быть удобно ссылаться на список с помощью дескриптора, который состоит из двух ссылок, указывающих на его первый и последний узлы.
Объединение альтернатив
Перечисленные выше альтернативы могут быть произвольно объединены почти во всех отношениях, поэтому можно иметь круговые двусвязные списки без часовых, круговые односвязные списки с часовыми и т.д.
Читайте также:




Комментарии
Отправить комментарий